ORTHOGONAUX (POLYNÔMES)

ORTHOGONAUX (POLYNÔMES)

C’est à travers l’étude de certains problèmes d’analyse fonctionnelle (équations intégrales, séries de Fourier, problème de Sturm-Liouville et, plus généralement, problèmes aux limites dans les équations aux dérivées partielles) qu’est apparue la notion de système orthogonal de fonctions. Ces problèmes amènent à considérer des espaces hermitiens constitués de fonctions et à déterminer les valeurs propres et les fonctions propres (cf. théorie SPECTRALE) de certains endomorphismes de ces espaces. Dans le cas d’un opérateur hermitien, les sous-espaces propres sont orthogonaux deux à deux. Le problème essentiel consiste alors à chercher des bases hilbertiennes constituées de fonctions propres.

Équation intégrale de Fredholm

Soit E un ensemble muni d’une mesure positive 猪 et k une fonction de carré intégrable sur E 憐 E. Pour toute fonction f de carré intégrable sur E et pour presque tout élément x de E, la fonction y 料 k (x , y ) f (y ) est intégrable sur E et la fonction g , définie presque partout par la formule:

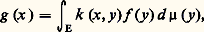est de carré intégrable sur E. L’application U^k , dite associée au noyau k , qui à tout élément f de L²(E) associe g , est un endomorphisme de L²(E). Lorsqu’on munit L²(E) de la norme de la convergence en moyenne quadratique, cet endomorphisme est continu et sa norme est inférieure à 瑩k 瑩²; cet endomorphisme est même un endomorphisme compact. La résolution de l’équation intégrale de Fredholm:

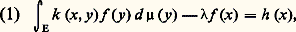où h est un élément donné de L²(E), conduit à chercher les valeurs propres et les vecteurs propres de l’endomorphisme U^k . Lorsque le noyau k est hermitien, c’est-à-dire lorsque, pour tout couple (x , y ) d’éléments de E, k (y , x ) = k (x , y ), alors l’endomorphisme compact U^k est hermitien. La théorie spectrale montre que l’ensemble sp(U^k ) des valeurs propres de U^k est une partie bornée dénombrable de R, dont tous les points, sauf peut-être 0, sont isolés. De plus, les sous-espaces propres E size=1^凞 sont orthogonaux deux à deux et le sous-espace vectoriel:

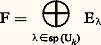est dense dans L²(E). Enfin, E est de dimension finie si 0. Il existe donc une suite (ⁿ ) de nombres réels convergeant vers 0 et une base hilbertienne ( 﨏ⁿ ) de L²(E) telles que, pour tout entier n , U^k ( 﨏ⁿ ) =ⁿ 﨏ⁿ . Une telle base ( 﨏ⁿ ) s’appelle système orthogonal associé au noyau k. Enfin, la suite (ⁿ ) est de carré sommable:

et le noyau k peut se développer de la manière suivante:

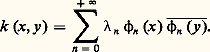Pour résoudre l’équation intégrale (1), on décompose le second membre h dans la base hilbertienne précédente:

Pour que: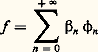

soit solution de (1), il faut et il suffit que, pour tout entier naturel n ,

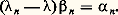En particulier, lorsque n’appartient pas à sp(U^k ) 聆0, l’équation (1) admet une solution et une seule. Lorsque 捻 sp(U^k ) 聆0, pour que (1) admette une solution, il faut et il suffit que h soit orthogonale au sous-espace vectoriel E size=1^凞. Enfin, lorsque = 0, pour que (1) admette une solution, il faut et il suffit que h soit orthogonale au noyau de U^k et que:

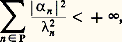où P désigne l’ensemble des entiers n tels queⁿ 0.

On notera que les séries précédentes convergent en moyenne quadratique. E. Schmidt (1907) et T. Mercer (1909) ont trouvé des conditions assez larges sous lesquelles la convergence est uniforme.

La théorie spectrale d’opérateurs hermitiens plus généraux conduit encore à des théories analogues. Signalons le cas des séries de Fourier (cf. analyse HARMONIQUE, espace de HILBERT) et celui des fonctions sphériques (cf. GROUPES - Groupes de Lie). Nous allons nous borner ici à un cas particulièrement simple.

Polynômes orthogonaux

Soit I un intervalle de R non réduit à un point et p une fonction à valeurs réelles continue sur I, telle qu’en tout point x intérieur à I, p (x ) 礪 0. Soit 暈^I(p ) l’espace vectoriel des fonctions f à valeurs complexes continues sur I telles que:

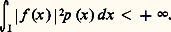On munit 暈^I(p ) du produit hermitien:

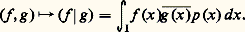L’espace hermitien 暈^I(p ) n’étant pas complet, on est amené à le considérer comme un sous-espace vectoriel L^2I(p ) des classes de fonctions f mesurables sur I à valeurs complexes et telles que:

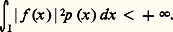Muni du produit hermitien précédent, L^2I(p ) est un espace hilbertien.

Plaçons-nous dans l’un des deux cas suivants:

a ) L’intervalle I est borné et p est intégrable sur I, c’est-à-dire que:

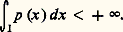b ) L’intervalle I est non borné, p est intégrable sur I et à décroissance rapide à l’infini, c’est-à-dire que, pour tout entier n ,

Les fonctions monomiales e ⁿ :x 料 x ⁿ appartiennent alors à 暈^I(p ). La suite (Pⁿ ) des fonctions polynomiales déduite de la famille (e ⁿ ) par orthonormalisation est appelée système de polynômes orthogonaux sur I associé au poids p ; pour tout entier naturel n , la suite (Pⁿ ) est un polynôme à coefficients réels de degré n , et le coefficient dominant de (Pⁿ ) est strictement positif.

Réciproquement, soit (Qⁿ ) une suite orthogonale de polynômes à coefficients complexes telle que, pour tout entier n , le polynôme Qⁿ soit de degré n. Pour tout entier n , il existe un nombre complexeⁿ et un seul tel que Qⁿ =ⁿ Pⁿ ; plus précisément: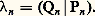

En utilisant le fait que Pⁿ est orthogonal à tout polynôme de degré inférieur ou égal à n 漣 1, on prouve facilement les résultats suivants:

Pour tout entier naturel non nul n , il existe un triplet ( 見ⁿ , 廓ⁿ , 塚ⁿ ) de nombres réels et un seul tel que:

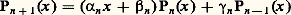(formule de récurrence linéaire à deux termes); en outre, 見ⁿ est strictement positif et 塚ⁿ strictement négatif.

Toutes les racines de Pⁿ sont réelles, simples et intérieures à I et, pour tout entier naturel non nul n , les racines de Pⁿ séparent celles de Pⁿ⁺¹ .

Enfin, lorsque l’intervalle I est symétrique par rapport à 0 et que la fonction p est paire, le polynôme Pⁿ est pair si n est pair, impair si n est impair, et 廓ⁿ = 0.

Il reste à examiner si la suite (Pⁿ ) est une base hilbertienne ou, ce qui revient au même, si le sous-espace vectoriel engendré par les fonctions e ⁿ est dense dans 暈^I(p ).

Lorsque l’intervalle I est borné, il en est toujours ainsi; cela résulte du théorème d’approximation de Weierstrass et du fait que, sur un intervalle borné, la convergence uniforme implique la convergence dans 暈^I(p ).

Lorsque l’intervalle I n’est pas borné, il peut arriver que (Pⁿ ) ne soit pas une base hilbertienne, par exemple si p (x ) = exp (face=F0019 漣|x | 見), où 見 捻 ]0, 1[. Cependant, lorsque p est à décroissance exponentielle, c’est-à-dire lorsque p est dominée par une fonction de la forme x 料 exp (face=F0019 漣 見|x |), où 見 礪 0, au voisinage de 梁 秊, la suite est une base hilbertienne de L(^2I p ) et a fortiori de 暈^I(p ). En effet, tous les moments Mⁿ = (f |e ⁿ ) d’un élément f de L^2I(p ) orthogonal aux polynômes Pⁿ sont nuls. D’autre part, la décroissance exponentielle du poids p permet de prouver que la bande de convergence de la transformée de Laplace de fp est non vide. On en déduit alors que fp est nulle presque partout et que f est nulle presque partout. Le problème de la recherche de conditions portant sur p pour que la suite (Pⁿ ) soit une base hilbertienne (problème de Bernstein) est assez délicat; il a fait l’objet de travaux de A. Denjoy (1922) et de T. Carleman (1932) et, plus récemment, de W. Pollard (1956) et de J.-P. Ferrier (1965), qui ont obtenu des conditions nécessaires et suffisantes.

Équations différentielles des polynômes orthogonaux

Soit I = [ 見, 廓] un intervalle compact de R, a et b deux fonctions à valeurs réelles indéfiniment dérivables sur I, la fonction a ne s’annulant pas sur l’intérieur de I et admettant un zéro simple aux points 見 et 廓. On considère l’équation différentielle:

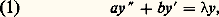où est un nombre complexe. De telles équations interviennent, par exemple, dans les problèmes de Sturm-Liouville. Les solutions de (1) sont les fonctions propres de l’endomorphisme U: f 料 af + bf de l’espace vectoriel E des fonctions indéfiniment dérivables sur I. Pour étudier l’équation (1), on introduit sa fonction résolvante, c’est-à-dire une fonction r à valeurs réelles strictement positives, définie sur l’intérieur de I vérifiant l’équation différentielle:

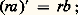alors:

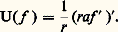Supposons que les nombres:

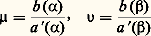soient réels strictement positifs. Dans ce cas, (x 漣 見) size=1^漣 size=1^猪r (x )a (x ) admet une limite finie non nulle au point 見 et ( 廓 漣 x ) size=1^漣 size=1^羽r (x )a (x ) admet une limite finie non nulle au point 廓. Par suite, pour tout couple (f, g ) d’éléments de E, la fonction rf 凜 est intégrable sur I.

On peut donc définir un produit hermitien sur E par la formule:

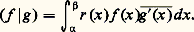L’endomorphisme U est alors hermitien; plus précisément:

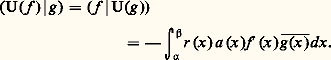Dans beaucoup de cas intervenant en pratique, on peut déterminer une base hilbertienne de E constituée de vecteurs propres de U. Nous nous contentons ici d’examiner le cas où a et b sont des fonctions polynomiales de la forme suivante:

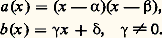Pour tout entier naturel n , le sous-espace vectoriel Eⁿ de E constitué des fonctions polynomiales de degré inférieur ou égal à n est stable par U. Les conditions 猪 礪 0 et 益 礪 0 sont équivalentes aux conditions 見塚 + 嗀 礪 0 et 廓塚 + 嗀 礪 0. De plus:

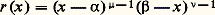est une résolvante de U. Le système (Pⁿ ) de polynômes orthogonaux associé au poids r est une base hilbertienne de E constituée de fonctions propres de U; plus précisément:

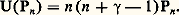Les polynômes Pⁿ s’appellent polynômes de Jacobi. Dans le cas où 猪 = 益 = 1, on trouve les polynômes de Legendre ; dans le cas où 猪 = 益 = 1/2, on trouve les polynômes de Tchebichev, ainsi que dans le cas où 猪 = 益 = 3/2.

Soit maintenant I un intervalle de la forme [ 見, + 秊[. On suppose cette fois que les fonctions a et b , ainsi que toutes leurs dérivées, sont des éléments de l’espace vectoriel E des fonctions à croissance lente au voisinage de + 秊, et on considère U comme un endomorphisme de E. On suppose que 猪 = b ( 見) / a ( 見) 礪 0 et que, d’autre part, b (x ) / a (x ) admet une limite strictement négative 益, finie ou infinie, lorsque x tend vers + 秊. Pour tout couple (f, g ) d’éléments de E, la fonction rf 凜 est alors intégrable sur I, et U est encore hermitien pour le produit hermitien précédemment défini. Lorsque a (x ) = x 漣 見 et que b (x ) = 塚x + 嗀, avec 塚 0, les conditions 猪 礪 0 et 益 麗 0 sont équivalentes aux conditions 塚 麗 0 et 塚見 + 嗀 礪 0. De plus,

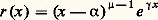est une résolvante de x. Le système (Pⁿ ) de polynômes orthogonaux associé au poids r est une base hilbertienne de E constituée de fonctions propres de U; plus précisément:

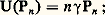les polynômes Pⁿ s’appellent polynômes de Sonine; dans le cas où 猪 = 1, on trouve les polynômes de Laguerre.

Examinons enfin le cas où I = R; on suppose que les fonctions a et b , ainsi que toutes leurs dérivées, sont des éléments de l’espace vectoriel E des fonctions à croissance lente au voisinage de 梁 秊, et on considère U comme un endomorphisme de E; on suppose de plus que b (x ) / a (x ) admet des limites 猪 礪 0 et 益 麗 0, finies ou infinies, lorsque x tend vers 漣 秊 et vers + 秊. La théorie se poursuit alors comme dans les cas précédents. Lorsqu’on a:

les conditions 猪 礪 0 et 益 麗 0 sont équivalentes à la condition 塚 麗 0. De plus: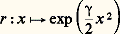

est une résolvante. Le système (Pⁿ ) des polynômes orthogonaux associé au poids r est encore une base hilbertienne de E constituée de fonctions propres de U; plus précisément:

les polynômes Pⁿ s’appellent alors polynômes d’Hermite.

Fonctions génératrices des polynômes orthogonaux

Les polynômes orthogonaux Pⁿ précédemment introduits peuvent se calculer de la manière suivante: de la relation (ra ) = rb , on déduit, par récurrence sur n , que: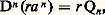

où Qⁿ est une fonction polynomiale de degré n. Par intégrations par parties, on prouve que, pour tout entier n , Qⁿ est proportionnel à Pⁿ : c’est la formule de Rodrigues. De plus, la résolvante r peut se prolonger en une fonction holomorphe sur C 漣 見, 廓. La formule intégrale de Cauchy permet alors d’établir la formule de Schläffli:

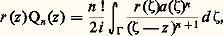où z 捻 C 漣 見, 廓 et où 臨 est un cercle d’indice 0 par rapport à 見 et 廓. On en déduit le résultat suivant (fonction génératrice des polynômes orthogonaux).

Soit x un point de I, et 福 un nombre réel strictement positif tel que le cercle 臨 de centre x et de rayon 福 soit d’indice 0 par rapport à 見 et 廓. Pour tout nombre complexe u tel que |u | sup |a ( 﨣)| 麗 福,

où w est le seul élément du disque ouvert de centre x et de rayon 福 tel que:

Dans le cas des polynômes de Legendre réduits, c’est-à-dire le cas où a (x ) = x ² 漣 1 et où b (x ) = 2 x , on peut prendre r = 1; le polynôme Qⁿ satisfait alors à l’équation différentielle: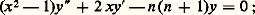

d’où:

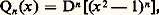et: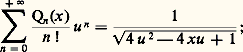

lorsque |u | 麗 1/6, cette série converge uniformément sur [ 漣 1, 1].

De même, la fonction génératrice des polynômes de Laguerre réduits, c’est-à-dire dans le cas où a (x ) = x et où b (x ) = 1 漣 x , est:

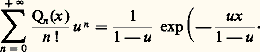Enfin, la fonction génératrice des polynômes d’Hermite réduits, c’est-à-dire dans le cas où a (x ) = 1 et b (x ) = 漣 2x , est:

Encyclopédie Universelle. 2012.